Feldspars
Feldspars are the most abundant mineral in the Earth's crust, making up more than 60% of both the continental crust and the oceanic crust. Understanding the relationship between their elastic properties and structure is especially crucial for understanding geophysical observations and for determining which aspects of crustal processes are really recorded by the cation partitioning patterns observed in feldspars.
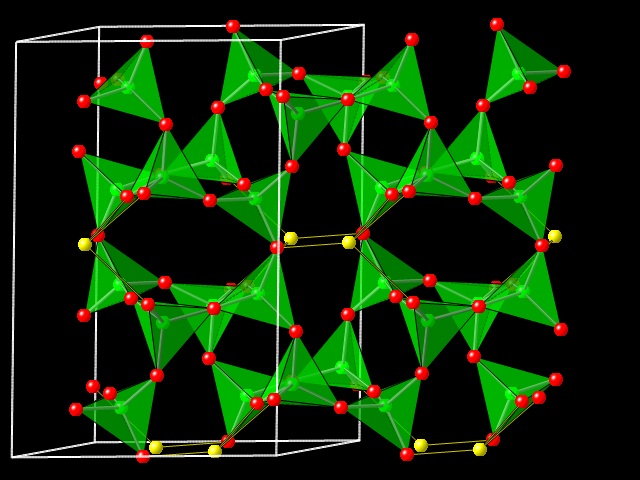
The feldspar structure consists of a three-dimensional framework of strongly-bonded TO4 tetrahedra formed by the sharing of oxygen atoms between tetrahedra with T being dominated by Al3+ and Si4+ in natural feldspars. Low-charge cations M occupy the larger voids in the tetrahedral framework to provide charge balance. Given that the tetrahedral framework of feldspars is truly three-dimensional and has no obvious layering, it is initially very surprising that feldspars respond extremely anisotropically to changes in pressure, temperature and the extra-framework cation. Between 60 and 70% of the volume change of all AlSi3 feldspars, both monoclinic and triclinic, induced by compositional change, temperature and pressure, is accommodated by change in the length of the (100) plane normal. This degree of anisotropy is as great as that of the sheet silicates, where the anisotropy clearly results from the bonding between the layers being significantly weaker than the strong bonding within the layers. But this cannot be the case for feldspars in which the T-O bonds are distributed more or less isotropically. It has long been known that the feldspar structure is relatively soft due to the intrinsic flexibility of the crankshaft chains of tetrahedra within the framework. However, the crankshafts are aligned along [100], so this does not explain the reason why the (100) plane normal exhibits the greatest strains with changes in temperature or extra-framework cation. In this page we describe the results of a project to simulate the structures of feldspars as a network of rigid tetrahedra, analyse the possible deformation mechanisms of the framework and thus show why feldspars are so anisotropic.
This work has been published in American Mineralogist by Angel, Sochalski-Kolbus and Tribaudino (2012). The tilted structures were generated from the untilted structure by using utilities within my cifReader program, which can also be used to calculate the tilts from any real feldspar structure. The analysis was aided greatly by the use of the CrystalMakerŽ software to make movies of the simulated structures. Further details are explored in Angel et al. (2013) in European Journal of Mineralogy. The CIFs of the structures discussed in that paper are in the Structure archive page.
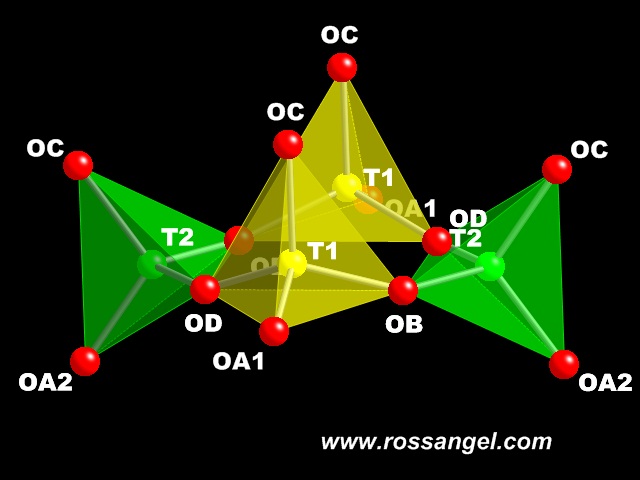 |
The key to understanding the feldspar structure is the basic building unit of the tetrahedral framework, which is the ring of 4 tetrahedra
shown here. It can undergo four different tilts of the tetrahedra that we show below. These four tilt systems do not deform the tetrahedra, and
we have simulated them with perfect regular tetrahedra in the monoclinic structure to calculate how the unit-cell parameters and volumes change
with the tilts. Similar tilts can occur in any ring of an even number of corner-shared tetrahedra, and are the basis of the structural evolution of not just feldspars but all structures made up of frameworks of tetrahedra. Therefore the techniques and ideas shown here can be easily extended to explain the behaviour of framework structures such as feldspathoids and zeolites. This is work on progress! To make the movies easier to follow, the T1 tetrahedra are shown in yellow, and the symmetrically distinct T2 tetrahedra are shown in green. |
| This is tilt #1, a tilt of the T1 tetrahedra around the Ob-Od edge. The movie shows a range of tilts from -20deg (outward tilt), through the untilted position, and on towards a +20deg inward tilt. Real feldspars normally have small positive (inward) tilts on average, which only vary between 0 and 5deg. | This is tilt #2, a tilt of the T2 tetrahedra around the Ob-Od edge in a similar manner to the #1 tilt. The movie only shows the tilts from the untilted structure to positive tilts, because in feldspars negative values of tilt #2 lead to very short distances between oxygen atoms. Real feldspars exhibit a large range of positive tilts. |
| Unlike the first two tilts, tilt #3 is a cooperative torsion of both the T1 and the T2 tetrahedra. The movie shows a range of tilts from the untilted position up to +30deg. Real feldspars exhibit a wide range of large positive tilts, which are strongly coupled with tilt #2. | Tilt #4 is a simple shear of the 4-ring. Alkali feldspars show very little change in this tilt, but there is a larger variation in the plagioclase feldspars. The movie shows tilts from -20 to +20 deg. |
|
Of the four possible tilt systems only two, #2 and #3 result in large changes in unit-cell volume. These are the two tilts that account for the structural changes in alkali feldspars at low pressures. Here is the #2 tilt viewed down [001]. The b-axis runs vertically, and the (100) plane normal runs horizontally. The (010) mirror plane of the monoclinic structure runs horizontally across the middle, and reflects the top half of the structure in to the bottom half. At one end of the movie loop you can see that the oxygen pairs across the mirror plane are very close together. That is why the #2 tilt is positive in all feldspars. By following the motion of the oxygen atoms at the corners of the tetrahedra you can easily see why this tilt gives rise to large change in all of the unit-cell parameters and a large change in volume. |
|
|
This is the #3 tilt shown in the same orientation as tilt #2 shown just above.
Compare the two movies carefully and you can see why both tilts lead to large changes in d(100) across the pictures, because of the motion of the apical Oc oxygens on the tops of the yellow T1 tetrahedra, which force the neighbouring rings along (100) apart. But this tilt #3 is a torsion which does not lead to the large rotations of the T2 tetrahedra seen with tilt #2 (above). Therefore the change in the vertical dimension in these movies (the b axis) decreases with tilt #3 but increases with tilt #2. So, different tilts of the 4-ring lead to different changes in the cell parameters of feldspars and different anisotropy of expansion and compression because the different tilts move the oygens that connect adjacent 4-rings in different ways. |
|
|
Large volume changes can only be accommodated in feldspars by tilts 2 and 3; this is because of the way in which the rings are linked together. Further analysis shows that the values of the tilts in feldspars maximise the shortest non-bonded O-O distances within the structure. For details see the paper by Angel, Sochalski-Kolbus and Tribaudino (2012).
The enormous anisotropy of feldspars is the result of this combination of tilts 2 and 3, as can be seen here. The movie shows the structural changes from Li-feldspar to Rb-feldspar. When both tilts operate together, you can see that d(100) (across the page) expands and contracts enormously, while the vertical direction (c-axis) hardly changes. The anisotropy is therefore a result of the framework topology and not a product of interaction with the extra-framework cations (seen here as purple spheres). |